Cacher is the code snippet organizer for pro developers

小 trick

overlap条件：start1 < end2 and end1 > start2

在DFS中我们说关键点是递归以及回溯，在BFS中，关键点则是状态的选取和标记

树算法

Binary Indexed Tree BIT 树状数组

class BIT:
    def __init__(self, n):
        self.n = n + 1
        self.sums = [0] * self.n

    def update(self, i, delta):
        while i < self.n:
            self.sums[i] += delta
            i += i & (-i) # = i & (~i + 1) 用于追踪最低位的1

    def prefixSum(self, i):
        res = 0
        while i > 0:
            res += self.sums[i]
            i -= i & (-i)
        return res

    def rangeSum(self, s, e):
        return self.prefixSum(e) - self.prefixSum(s - 1)

Binary Search Tree

class Node(object):
    def __init__(self, data):
        self.left = None
        self.right = None
        self.data = data

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def search(self, data, parent=None):
        if data < self.data:
            if self.left is None:
                return None, None
            return self.left.search(data, self)
        elif data > self.data:
            if self.right is None:
                return None, None
            return self.right.search(data, self)
        else:
            return self, parent

Trie

import collections

class TrieNode():
    def __init__(self):
        self.children = collections.defaultdict(TrieNode)
        self.isEnd = False

class Trie():
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        node = self.root
        for w in word:
            node = node.children[w]
        node.isEnd = True

    def search(self, word):
        node = self.root
        for w in word:
            # dict.get() 找不到的话返回None
            node = node.children.get(w)
            if not node:
                return False
        return node.isEnd

线段树

class SegmentTree(object):
    def __init__(self, nums, s=None, e=None):  # build
        self.lo, self.hi = s, e
        self.left, self.right = None, None

        self.mid = (self.lo+self.hi)/2
        self.val = 0

        if self.hi < self.lo:
            return
        elif self.hi == self.lo:
            self.val = nums[self.lo]
        else:  # self.lo < self.hi
            self.left = SegmentTree(nums, self.lo, self.mid)
            self.right = SegmentTree(nums, self.mid+1, self.hi)
            self.val = self.left.val + self.right.val

    def update(self, i, val):  # modify
        if i == self.lo == self.hi:
            self.val = val
        else:
            if i <= self.mid:
                self.left.update(i, val)
            else:
                self.right.update(i, val)
            self.val = self.left.val + self.right.val

    def sumRange(self, i, j):  # query
        if i == self.lo and j == self.hi:  # equal
            return self.val
        elif self.lo > j or self.hi < i:  # not intersect
            return 0
        else:  # intersect
            if i > self.mid:  # all at the right sub tree
                return self.right.sumRange(i, j)
            elif j <= self.mid:  # all at the left sub tree
                return self.left.sumRange(i, j)
            else:  # some at the right & some at the left
                return self.left.sumRange(i, self.mid) + self.right.sumRange(self.mid+1, j)

    def get(self, i):
        if self.lo == self.hi == i:
            return self.val
        elif self.lo > i or self.hi < i:
            return 0
        else:
            if i > self.mid:  # right
                return self.right.get(i)
            else:  # left
                return self.left.get(i)

排序算法

快速选择

quick select

def partition(nums, lo, hi):
    i, x = lo, nums[hi]
    for j in range(lo, hi):
        if nums[j] <= x:
            nums[i], nums[j] = nums[j], nums[i]
            i += 1
    nums[i], nums[hi] = nums[hi], nums[i]
    return i

def quick_select(nums, lo, hi, k):
    while lo < hi:
        mid = partition(nums, lo, hi)
        if mid == k:
            return nums[k]
        elif mid < k:
            lo = mid+1
        else:
            hi = mid-1

nums = [54, 26, 93, 17, 77, 31, 44, 55, 20]
for i in range(len(nums)):
    print(quick_select(nums, 0, len(nums)-1, i))

selection sort

def selection_sort(nums):
    for i in range(len(nums), 0, -1):
        tmp = 0
        for j in range(i):
            if not compare(nums[j], nums[tmp]):
                tmp = j
        nums[tmp], nums[i-1] = nums[i-1], nums[tmp]
    return nums

quick sort, in-place

def quick_sort(nums, l, r):
    if l >= r:
        return
    pos = partition(nums, l, r)
    quick_sort(nums, l, pos-1)
    quick_sort(nums, pos+1, r)

def partition(nums, lo, hi):
    i, x = lo, nums[hi]
    for j in range(lo, hi):
        if nums[j] <= x:
            nums[i], nums[j] = nums[j], nums[i]
            i += 1
    nums[i], nums[hi] = nums[hi], nums[i]
    return i

arr = [4, 2, 1, 23, 2, 4, 2, 3]
quick_sort(arr, 0, len(arr)-1)
print(arr)

bubble sort

def bubble_sort(nums):
    for i in reversed(range(len(nums))):
        for j in range(i-1):
            if not compare(nums[j], nums[j+1]):
                nums[j], nums[j+1] = nums[j+1], nums[j]
    return nums

insertion sort

def insertion_sort(nums):
    for i in range(len(nums)):
        pos, cur = i, nums[i]
        while pos > 0 and not compare(nums[pos-1], cur):
            nums[pos] = nums[pos-1]  # move one-step forward
            pos -= 1
        nums[pos] = cur
    return nums

merge sort

def merge_sort(nums):
    nums = mergeSort(nums, 0, len(nums)-1)
    return str(int("".join(map(str, nums))))

def mergeSort(nums, l, r):
    if l > r:
        return
    if l == r:
        return [nums[l]]
    mid = (r+l)//2
    left = mergeSort(nums, l, mid)
    right = mergeSort(nums, mid+1, r)
    return merge(left, right)

def merge(l1, l2):
    res, i, j = [], 0, 0
    while i < len(l1) and j < len(l2):
        if not compare(l1[i], l2[j]):
            res.append(l2[j])
            j += 1
        else:
            res.append(l1[i])
            i += 1
    res.extend(l1[i:] or l2[j:]) # 喵🐱
    return res

图论算法

拓扑排序

两个defaultdict 一个graph，一个in_degree

from collections import defaultdict

def findOrder(numCourses, prerequisites):
    graph = defaultdict(list)
    in_degree = defaultdict(int)

    for dest, src in prerequisites:
        graph[src].append(dest)
        in_degree[dest] += 1

    zero_degree = [k for k, v in in_degree.items() if v == 0]
    res = []
    while zero_degree:
        node = zero_degree.pop(0)
        res.append(node)
        for child in graph[node]:
            in_degree[child] -= 1
            if in_degree[child] == 0:
                zero_degree.append(child)  # 同时也说这个元素该删除了

    return res

普利姆（Prime）算法

每个节点选cost最小的边

from collections import defaultdict
import heapq

def prim(vertexs, edges):
    adjacent_vertex = defaultdict(list)
    for v1, v2, length in edges:
        adjacent_vertex[v1].append((length, v1, v2))
        adjacent_vertex[v2].append((length, v2, v1))

    """
    经过上述操作，将edges列表中各项归类成以某点为dictionary的key，其value则是其相邻的点以及边长。如下：
    defaultdict(<type 'list'>, {'A': [(7, 'A', 'B'), (5, 'A', 'D')],
                                'C': [(8, 'C', 'B'), (5, 'C', 'E')],
                                'B': [(7, 'B', 'A'), (8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E')],
                                'E': [(7, 'E', 'B'), (5, 'E', 'C'), (15, 'E', 'D'), (8, 'E', 'F'), (9, 'E', 'G')],
                                'D': [(5, 'D', 'A'), (9, 'D', 'B'), (15, 'D', 'E'), (6, 'D', 'F')],
                                'G': [(9, 'G', 'E'), (11, 'G', 'F')],
                                'F': [(6, 'F', 'D'), (8, 'F', 'E'), (11, 'F', 'G')]})
    """

    res = []  # 存储最小生成树结果

    # vertexs是顶点列表，vertexs = list("ABCDEFG") == = > vertexs = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
    visited = set(vertexs[0])

    # 得到adjacent_vertexs_edges中顶点是'A'（nodes[0]='A')的相邻点list，即adjacent_vertexs['A']=[(7,'A','B'),(5,'A','D')]
    adjacent_vertexs_edges = adjacent_vertex[vertexs[0]]

    # 将usable_edges加入到堆中，并能够实现用heappop从其中动态取出最小值。关于heapq模块功能，参考python官方文档
    heapq.heapify(adjacent_vertexs_edges)

    while adjacent_vertexs_edges:
        # 得到某个定点（做为adjacent_vertexs_edges的键）与相邻点距离（相邻点和边长/距离做为该键的值）最小值
        w, v1, v2 = heapq.heappop(adjacent_vertexs_edges)
        if v2 not in visited:
            # 在used中有第一选定的点'A'，上面得到了距离A点最近的点'D',举例是5。将'd'追加到used中
            visited.add(v2)

            # 将v1,v2,w，第一次循环就是('A','D',5) append into res
            res.append((v1, v2, w))

            # 再找与d相邻的点，如果没有在heap中，则应用heappush压入堆内，以加入排序行列
            for next_vertex in adjacent_vertex[v2]:
                if next_vertex[2] not in visited:
                    heapq.heappush(adjacent_vertexs_edges, next_vertex)
    return res

# test
vertexs = list("ABCDEFG")
edges = [("A", "B", 7), ("A", "D", 5),
         ("B", "C", 8), ("B", "D", 9),
         ("B", "E", 7), ("C", "E", 5),
         ("D", "E", 15), ("D", "F", 6),
         ("E", "F", 8), ("E", "G", 9),
         ("F", "G", 11)]

print("edges:", edges)
print("prim:", prim(vertexs, edges))

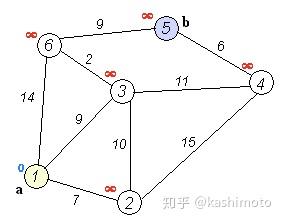
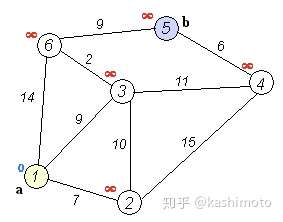
Dijkstra[单源最短路径算法]

• Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径
• 以起始点为中心向外层层扩展，直到扩展到终点为止
• 要求图中不存在负权边

import sys

def dijkstra(graph):
    n = len(graph)
    dist = [sys.maxsize] * n
    dist[0] = 0  # 自己和自己距离为0
    visited = set()

    def minDistance():
        # 找到还没确定的里面距离最小的
        min_ans, min_index = min((dis, i)
                                 for i, dis in enumerate(dist) if i not in visited)
        return min_index

    for _ in range(n):
        min_index = minDistance()
        # 已经确定了
        visited.add(min_index)
        for v in range(n):
            if v not in visited and graph[min_index][v] > 0:
                # graph[min_index][v] > 0 表示存在这个路径
                new_dist = dist[min_index] + graph[min_index][v]
                if dist[v] > new_dist:  # 表示值得被更新
                    dist[v] = new_dist

    print(dist)

# Driver program
graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
         [4, 0, 8, 0, 0, 0, 0, 11, 0],
         [0, 8, 0, 7, 0, 4, 0, 0, 2],
         [0, 0, 7, 0, 9, 14, 0, 0, 0],
         [0, 0, 0, 9, 0, 10, 0, 0, 0],
         [0, 0, 4, 14, 10, 0, 2, 0, 0],
         [0, 0, 0, 0, 0, 2, 0, 1, 6],
         [8, 11, 0, 0, 0, 0, 1, 0, 7],
         [0, 0, 2, 0, 0, 0, 6, 7, 0]]

dijkstra(graph)

Floyd[任意两点间的最短路径]

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

Inf = 65535  # 代表无穷大
arr = [[0, 10, Inf, Inf, Inf, 11, Inf, Inf, Inf],  # 邻接矩阵
       [10, 0, 18, Inf, Inf, Inf, 16, Inf, 12],
       [Inf, 18, 0, 22, Inf, Inf, Inf, Inf, 8],
       [Inf, Inf, 22, 0, 20, Inf, Inf, 16, 21],
       [Inf, Inf, Inf, 20, 0, 26, Inf, 7, Inf],
       [11, Inf, Inf, Inf, 26, 0, 17, Inf, Inf],
       [Inf, 16, Inf, 24, Inf, 17, 0, 19, Inf],
       [Inf, Inf, Inf, 16, 7, Inf, 19, 0, Inf],
       [Inf, 12, 8, 21, Inf, Inf, Inf, Inf, 0]]

n = len(arr)  # 邻接矩阵大小
path = [[-1]*n for _ in range(n)]

for k in range(n): # k在第一层
    for i in range(n):
        for j in range(n):
            if(arr[i][j] > arr[i][k]+arr[k][j]):  # 两个顶点直接较小的间接路径替换较大的直接路径
                arr[i][j] = arr[i][k]+arr[k][j]
                path[i][j] = k  # 记录新路径的前驱
for x in arr:
    print(x)
print()
for x in path:
    print(x)

字符串算法

KMP

class Solution(object):
    def strStr(self, haystack, needle):
        """
        :type haystack: str
        :type needle: str
        :rtype: int
        """
        if not needle: return 0
        # build next
        next = [0]*len(needle)
        l, r = 0, 1
        while r < len(needle):
            if needle[l] == needle[r]:
                next[r] = l+1
                l, r = l+1, r+1
            elif l: l = next[l-1]
            else: r += 1
        # find idx
        l, r = 0, 0
        while r < len(haystack):
            if needle[l] == haystack[r]:
                if l == len(needle)-1:
                    return r-l
                l, r = l+1, r+1
            elif l: l = next[l-1]
            else: r += 1
        return -1

Rabin-Karp Hash

class RabinKarpHash:
    def __init__(self, base, mod=int(1e9+7)):
        self.base = base
        self.mod = mod

    def hash(self, arr):
        h = 0
        for val in arr:
            h = ((h * self.base) + val) % self.mod
        return h

    def roll(self, origin_hash, drop_val, new_val, max_base):
        h = origin_hash - (drop_val * max_base % self.mod)
        h = ((h*self.base)+new_val+self.mod)%self.mod
        return h

    def get_max_base(self, length):
        ret = 1
        for i in range(length-1):
            ret = (ret*self.base) % self.mod
        return ret

Manacher’s Algorithm

https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-4/

def findLongestPalindromicString(text):
    length = len(text)
    if length == 0:
        return
    N = 2*length+1    # Position count
    L = [0] * N
    L[0] = 0
    L[1] = 1
    C = 1     # centerPosition
    R = 2     # centerRightPosition
    i = 0    # currentRightPosition
    iMirror = 0     # currentLeftPosition
    maxLPSLength = 0
    maxLPSCenterPosition = 0
    diff = -1

    for i in range(2, N):
        # get currentLeftPosition iMirror for currentRightPosition i
        iMirror = 2*C-i
        L[i] = 0  # 初始化范围
        diff = R - i  # 当前位置离上一个边界的距离
        # If currentRightPosition i is within centerRightPosition R
        if diff > 0:  # 利用对称性获取L[i]的最小值
            L[i] = min(L[iMirror], diff)

        # 计算当前palindrome长度
        while (True):
            # 边界条件
            con1 = (i + L[i]) < N and (i - L[i]) > 0
            if (not con1):
                break

            # 奇数位置需要比较char
            # 偶数位置直接加一
            con2 = (i + L[i]) % 2 == 1
            left_radius = int((i + L[i] + 1) / 2)
            right_radius = int((i - L[i] - 1) / 2)
            con31 = 0 <= left_radius and left_radius < length
            con32 = 0 <= right_radius and right_radius < length
            con3 = con31 and con32 and (text[left_radius] == text[right_radius])
            if(con2 or con3):
                L[i] += 1
            else:
                break

        if L[i] > maxLPSLength:        # Track maxLPSLength
            maxLPSLength = L[i]
            maxLPSCenterPosition = i

        # 触及上一个边界的话选择center
        if i + L[i] > R:
            C = i
            # 更新边界为当前的边界
            R = i + L[i]

    # Uncomment it to print LPS Length array
    # printf("%d ", L[i]);
    start = int((maxLPSCenterPosition - maxLPSLength) / 2)
    end = int(start + maxLPSLength)
    print(text[start:end])

# Driver program
text1 = "babcbabcbaccba"
findLongestPalindromicString(text1)

链表相关

优雅地遍历链表

while head:
    head = head.next

standard linked list reversing

class Solution:
    def reverseList(self, head):
        cur, prev = head, None
        while cur:
            cur.next, cur, prev = prev, cur.next, cur  # standard reversing
        return prev

merge sort list

class Solution(object):
    def merge(self, h1, h2):
        dummy = tail = ListNode(None)
        while h1 and h2:
            if h1.val < h2.val:
                tail.next, tail, h1 = h1, h1, h1.next
            else:
                tail.next, tail, h2 = h2, h2, h2.next

        tail.next = h1 or h2
        return dummy.next

    def sortList(self, head):
        if not head or not head.next:
            return head

        pre, slow, fast = None, head, head
        while fast and fast.next:
            pre, slow, fast = slow, slow.next, fast.next.next
        pre.next = None

        return self.merge(self.sortList(head), self.sortList(slow))

二分

标准二分（bisect）

永远是lo = mid+1， hi = mid，返回lo,lo=0, hi=n

# 等价于 bisect
# 保证 选的数>k 严格大于
def bisect_right(a, x, lo=0, hi=None):
    lo, hi = 0, n
    while lo < hi:
        mid = (lo+hi)//2
        if x < a[mid]:
            hi = mid # disgard equals part
        else:
            lo = mid+1
    return lo

# bisect_left is more useful at hand, since it returns the exact index of the element being looked up if it is present in the list
# 保证 选的数>=k 大于等于
def bisect_left(a, x, lo=0, hi=None):
    lo, hi = 0, n
    while lo < hi:
        mid = (lo+hi)//2
        if a[mid] < x:
            lo = mid+1  # disgard equals part
        else:
            hi = mid
    return lo

>>> import bisect
>>> bisect.bisect_left([1,2,3], 2)
1
>>> bisect.bisect_right([1,2,3], 2)
2

范围都是[0-n]

import bisect
print(bisect.bisect_left([1, 2, 3], -1))  # 0
print(bisect.bisect_left([1, 2, 3], 0))  # 0
print(bisect.bisect_left([1, 2, 3], 1))  # 0
print(bisect.bisect_left([1, 2, 3], 2))  # 1
print(bisect.bisect_left([1, 2, 3], 3))  # 2
print(bisect.bisect_left([1, 2, 3], 4))  # 3

print(bisect.bisect([1, 2, 3], -1))  # 0
print(bisect.bisect([1, 2, 3], 0))  # 0
print(bisect.bisect([1, 2, 3], 1))  # 1
print(bisect.bisect([1, 2, 3], 2))  # 2
print(bisect.bisect([1, 2, 3], 3))  # 3
print(bisect.bisect([1, 2, 3], 4))  # 3

二分最优问题

都是 (lo+hi)//2， helper(mid) >= K， hi = mid-1， lo = mid+1

# 最大
# 找到最大的mid使得helper(mid)>=K
lo, hi = 1, sum(sweetness)
while lo <= hi:
    # 找到最大的mid使得count>=K
    mid = (lo+hi)//2
    if helper(mid) >= K:  # mid还可以再大一点
        lo = mid+1
    else:
        hi = mid-1
    return hi # 返回的是hi

# 最小
# 找到最小的mid使得helper(mid)>=K
lo, hi = 1, sum(sweetness)
while lo <= hi:
    # 找到最大的mid使得count>=K
    mid = (lo+hi)//2
    if helper(mid) >= K:  # mid还可以再大一点
        hi = mid-1
    else:
        lo = mid+1
    return lo # 返回的是lo

搜索算法

并查集 Union-Find Set (General)

class UF:
    def __init__(self, n):
        self.parent = list(range(n+1))

    def find(self, i):
        if self.parent[i] != i:  # 用i来判断
            self.parent[i] = self.find(self.parent[i])  # 路径压缩
        return self.parent[i]

    def union(self, x, y):
        self.parent[self.find(x)] = self.find(y)

回溯法通用模板

def combine(self, n, k):
    ans = []

    def helper(cur, start):
        if len(cur) == k:
            ans.append(cur[:])
            return
        else:
            for i in range(start+1, n+1):
                cur.append(i)
                helper(cur, i)
                cur.pop()

    helper([], 0)
    return ans

A星算法核心公式

F = G + H

F - 方块的总移动代价 G - 开始点到当前方块的移动代价 H - 当前方块到结束点的预估移动代价[heuristic]

import heapq

def heuristic(a, b):
    return (b[0] - a[0]) ** 2 + (b[1] - a[1]) ** 2

def astar(array, start, destination):
    n, m = len(array), len(array[0])
    dirs = [(0, 1), (0, -1), (1, 0), (-1, 0),
            (1, 1), (1, -1), (-1, 1), (-1, -1)]

    visited = set()
    came_from = {}
    gscore = {start: 0}
    fscore = {start: heuristic(start, destination)}
    queue = []

    heapq.heappush(queue, (fscore[start], start))

    while queue:
        score, cur_pos = heapq.heappop(queue)

        if cur_pos == destination:
            data = []
            while cur_pos in came_from:
                data.append(cur_pos)
                cur_pos = came_from[cur_pos]
            return data

        visited.add(cur_pos)
        for i, j in dirs:
            x, y = cur_pos[0] + i, cur_pos[1] + j
            neibor = (x, y)
            g = gscore[cur_pos]
            h = heuristic(cur_pos, neibor)
            f = g+h
            if (not(0 <= x < n and 0 <= y < m)  # 不能越界
                    or array[x][y] == 1  # 墙不能走
                    or(neibor in visited and f >= gscore.get(neibor, 0))):  # 还不如从0直接过来
                continue

            if g < gscore.get(neibor, 0) or neibor not in [i[1]for i in queue]:
                came_from[neibor] = cur_pos
                gscore[neibor] = g
                fscore[neibor] = g + \
                    heuristic(neibor, destination)
                heapq.heappush(queue, (fscore[neibor], neibor))

    return False

nmap = [
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

print(astar(nmap, (0, 0), (10, 13)))

def heuristic(a, b):
    (x1, y1) = a
    (x2, y2) = b
    return abs(x1 - x2) + abs(y1 - y2)

def a_star_search(graph, start, goal):
    frontier = PriorityQueue()
    frontier.put(start, 0)
    came_from = {}
    cost_so_far = {}
    came_from[start] = None
    cost_so_far[start] = 0

    while not frontier.empty():
        current = frontier.get()

        if current == goal:
            break

        for next in graph.neighbors(current):
            new_cost = cost_so_far[current] + graph.cost(current, next)
            if next not in cost_so_far or new_cost < cost_so_far[next]:
                cost_so_far[next] = new_cost
                priority = new_cost + heuristic(goal, next)
                frontier.put(next, priority)
                came_from[next] = current

    return came_from, cost_so_far

数学方法

素数筛法

# 1不是素数，最小的质数是2
# Prime table
maxInteger = 1000000
prime = [True]*maxInteger
prime[0] = False
prime[1] = False
for i in range(2, (int)(math.sqrt(maxInteger)+1)):
    if prime[i]:
        for j in range(i*i, maxInteger, i):
            prime[j] = False

求因数

# Given a list A, return all prime factors of elements in A
def getAllFactors(A):
    factors = []
    for x in A:
        facs = []
        # 筛法优化
        k, d = 0, primes[k]
        while d * :
            if x % d == 0:
                while x % d == 0:
                    x //= d
                facs.append(d)
            k += 1
            d = primes[k]
        # 特判，x>1说明有残余的质数，not facs说明x本身是质数
        if x > 1 or not facs:
            facs.append(x)
        factors.append(facs)

黄金比例求斐波那契

class Solution:
  def fib(self, N):
    golden_ratio = (1 + 5 ** 0.5) / 2
    return int((golden_ratio ** N + 1) / 5 ** 0.5)

$$ \phi=\frac{1+\sqrt{5}}{2} \approx 1.61803 $$

快速幂

def fastExpMod(a, b):
    res = 1
    while b:
        if (b & 1):
            # ei = 1, then mul
            res *= a
        b >>= 1
        # b, b^2, b^4, b^8, ... , b^(2^n)
        a *= a
    return res

牛顿法

class Solution:
    def mySqrt(self, x):
        r = x + 1  # avoid dividing 0
        while r*r > x:
            r = int((r+x/r)/2)  # newton's method
        return r

GCD

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

求多个数的GCD

def arr_gcd(self, A):
    gcd = A[0]
    for a in A:
        while a:
            gcd, a = a, gcd % a
    return gcd

graycode

def grayCode(n):
    res = [0]
    i = 0
    while i < n:  # 从2的0次方开始，
        next_base = 1 << i
        res_inv = [x + next_base for x in reversed(res)]
        res.extend(res_inv)
        i += 1
    return res

# 长度为4的所有graycode
# 用于遍历所有情况
# 0000
# 0001
# 0011
# 0010
# 0110
# 0111
# 0101
# 0100
# 1100
# 1101
# 1111
# 1110
# 1010
# 1011
# 1001
# 1000

专用方法

单调栈

def foo(nums):
    st = []
    res = [0]*len(nums)
    for i, x in enumerate(nums):
        while st and nums[st[-1]] < x:
            idx = st.pop()
            res[idx] = i-idx
        st.append(i)
    return res

slide window

一个for 一个 while 不容易出错

class Window:
    def __init__(self):
        self.count = collections.Counter()
        self.reserve = 0

    def add(self, x):
        if self.count[x] == 0: # 从效果上来判断
            self.reserve += 1
        self.count[x] += 1

    def remove(self, x):
        self.count[x] -= 1
        if self.count[x] == 0: #
            self.reserve -= 1

class Solution(object):
    def lengthOfLongestSubstringKDistinct(self, A, K):
        if not A or not len(A) or not K:
            return 0

        win = Window()

        ans = l = 0
        # 一个for 一个 while 不容易出错
        for r, x in enumerate(A):
            win.add(x)

            while win.reserve > K:
                win.remove(A[l])
                l += 1

            ans = max(r-l+1, ans)

        return ans

二维数组前缀和

n, m = len(grid), len(grid[0])
pre_sum = [[0]*(m+1) for _ in range(n+1)]

for i in range(n):
    for j in range(m):
        pre_sum[i][j] = pre_sum[i][j-1] + \
            pre_sum[i-1][j] - pre_sum[i-1][j-1] + grid[i][j]

def get_sum(x0, y0, x1, y1):
    return pre_sum[x1][y1] - pre_sum[x0-1][y1] - pre_sum[x1][y0-1] + pre_sum[x0-1][y0-1]

def helper(size):
    cur_max_sum = max(get_sum(x, y, x+size-1, y+size-1)
                        for x in range(n-size+1) for y in range(m-size+1))
    return cur_max_sum

RMQ/ST[Sparse Table]算法

import math

class ST:

    def __init__(self, arr):
        self.arr = arr
        self.n = n = len(arr)
        self.m = m = int(math.log(n, 2))

        self.maxsum = maxsum = [[0]*(m+1) for _ in range(n)]
        self.minsum = minsum = [[0]*(m+1) for _ in range(n)]

        for i, x in enumerate(arr):
            maxsum[i][0] = minsum[i][0] = x

        for j in range(m):
            for i in range(n):
                k = i + (1 << j)
                if(k < n):
                    maxsum[i][j+1] = max(
                        maxsum[i][j], maxsum[k][j])
                    minsum[i][j+1] = min(
                        minsum[i][j], minsum[k][j])

    def get_max(self, a, b):
        k = int(math.log(b-a+1, 2))
        # 一头一尾
        return max(self.maxsum[a][k], self.maxsum[b-(1 << k)+1][k])

    def get_min(self, a, b):
        k = int(math.log(b-a+1, 2))
        return min(self.minsum[a][k], self.minsum[b-(1 << k)+1][k])

arr = [3, 4, 5, 7, 8, 9, 0, 3, 4, 5]
st = ST(arr)
print(st.get_max(0, 9))  # 9
print(st.get_max(6, 9))  # 5
print(st.get_min(0, 9))  # 0
print(st.get_min(0, 4))  # 3

LZ77

def compress(message):
    win_size = 10  # 窗口长度
    pointer = 0  # 指针，初始指向第一个位置
    compressed_message = []
    while pointer < len(message):
        matched_length = 0  # 匹配到的长度

        # 窗口的corner case
        window = message[max(pointer - win_size, 0):pointer]

        # 能找到的最大长度
        while window.find(message[pointer:pointer + matched_length + 1]) != -1:
            matched_length += 1
        e = pointer + matched_length

        # window.find(message[start:end]) 相对窗口的offset
        # max(start - win_size, 0) 整个窗口的offset
        # first：在整个字符串中的offset
        first_appear = window.find(message[pointer:e]) + \
            max(pointer - win_size, 0)

        item = (pointer - first_appear, matched_length, message[e])
        compressed_message.append(item)
        pointer += matched_length + 1

    return compressed_message

print(compress("abcdbbccaaabaeaaabaee"))

优雅地先序遍历

def preorder(self, root):
    if (not root):
        return ["null"]
    return [str(root.val)]+self.preorder(root.left)+self.preorder(root.right)

def serialize(self, root):
    return ",".join(self.preorder(root))